En matemáticas, una función polinómica es una función asociada a un polinomio con coeficientes en un anillo conmutativo (a menudo un cuerpo).
Formalmente, es una función:

- donde
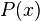 es un polinomio definido para todo número real
es un polinomio definido para todo número real  ; es decir, una suma finita de potencias de
; es decir, una suma finita de potencias de  multiplicados por coeficientes reales, de la forma:1
multiplicados por coeficientes reales, de la forma:1
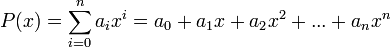
Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:
| Grado | Nombre | Expresión |
|---|---|---|
| 0 | función constante | y = a |
| 1 | función lineal | y = ax + b es un binomio del primer grado |
| 2 | función cuadrática | y = ax² + bx + c es un trinomio del segundo grado |
| 3 | función cúbica | y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado |
Representación gráfica de funciones polinómicas de grado cero
La gráfica de una función polinomial de grado 0, que es de la forma f(x) = a es una recta horizontal.

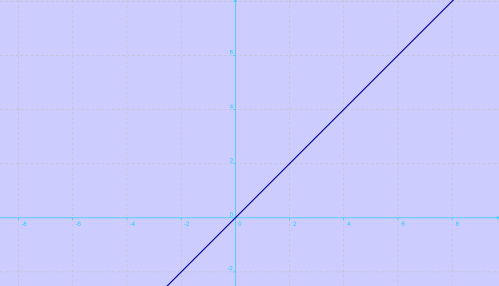
Representación gráfica de funciones polinómicas de grado uno
La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de forma oblicua.
y = m x + b
Representación gráfica de funciones polinómicas de grado 2
Las funciones polinómicas de grado 2 son del tipo  , con
, con  . Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de
. Sus representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que dependen del signo de  . Son éstas:
. Son éstas:
 |  |
Representación gráfica de funciones polinómicas de grado 3
Las funciones polinómicas de grado 3 son del tipo 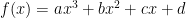 , con
, con  . Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de
. Hay cuatro posibles representaciones gráfica de este tipo de funciones que dependen del signo de  y de la relación entre
y de la relación entre 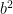 y
y  . Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
. Por tanto, para poder representarlas debemos tener en cuenta sus coeficientes. Os dejo una tabla con las cuatro gráficas posibles:
 |  | |
 |  |
Vallasa a la verga perros
ResponderEliminarbuena informacion,gracias
ResponderEliminar